Last year, when tutoring a student through how ligands interact with the d orbitals of metals center, I was annoyed to realize that there was no easily accessible d orbital viewer with point charges to represent the ligands. This would have greatly helped explain this concept to my student as it shows in 3D, not 2D like all the online resources I was able to find, that different ligand configurations lead to the raising and lowering of orbital energies via the overlap of the ligand with the orbital. While the 2D representations are helpful; not being able to view all of the ligands at once and having to mentally translate it into a 3D representation presented road blocks that just don’t need to be there when teaching this topic. Therefore, I set out to build a d Orbital Viewer in the hopes others will find it useful.
To start off with I needed the d orbitals. For this I used the d orbitals obtained from the solutions to the hydrogen atom available in an analytical form. These solutions are expressed as:
Where is the principle quantum number representing what shell each orbital corresponds to (ex.
= 1 and 2 for the first and second row orbitals of the periodic table respectively),
is the angular momentum quantum number corresponding to the subshell (ex.
= 1 and 2 are the s and p orbital labels), and
is the magnetic quantum number denoting the different orbitals in each subshell. For this work I utilized the lowest energy d orbitals, the 3d orbitals. From our general form of the hydrogenic wavefunction these occur when
= 3 and
= 2 and the
quantum number is allowed to vary. Here are the solutions expressed in spherical coordinates:
Instead of translating the spherical coordinates, , into the cartesian
, I sample points in cartesian space and translate them into spherical coordinates for use with the above equations. I do this as:
where:
More information about this transformation can be found on Wikipedia here, while more information about arctan2 function used to implement the in a quadrant aware way can be found here and here.
The code implementing the above is:
def hydrogen_den(X,Y,Z):
R = np.sqrt(X**2+Y**2+Z**2)
if R == 0:
return 0
Theta = np.arccos(Z/R)
Phi = np.arctan2(Y,X)
#l=2 m=0
#wf = 1/(81*sqrt(6*pi))*R**2.*exp(-R/3)*(3*cos(Theta)**2-1)
#l=2 m=+-1
#wf = 1/(81*sqrt(pi))*R**2*exp(-R/3)*sin(Theta)*cos(Theta)*exp(1j*Phi)
wf = 1/(81*sqrt(pi))*R**2*exp(-R/3)*sin(Theta)*cos(Theta)*exp(-1j*Phi)
#l=2 m=+-2
#wf = 1/(162*sqrt(pi))*R**2*exp(-R/3)*sin(Theta)**2*exp(2j*Phi)
#wf = 1/(162*sqrt(pi))*R**2*exp(-R/3)*sin(Theta)**2*exp(-2j*Phi)
return (wf*np.conj(wf)).realThis function takes in coordinates in cartesian space, converts them to spherical coordinates, calculates the desired 3d orbital based on what wf = is not commented out, and lastly obtains the electronic density by multiplying the resulting wavefunction value by its complex conjugate. To suppress a numpy warning I return just the real part of the result (Although there shouldn’t have been any complex component left anyway).
Strange solutions?
If we were to just view the density of each wavefunction above we’d get these as results:
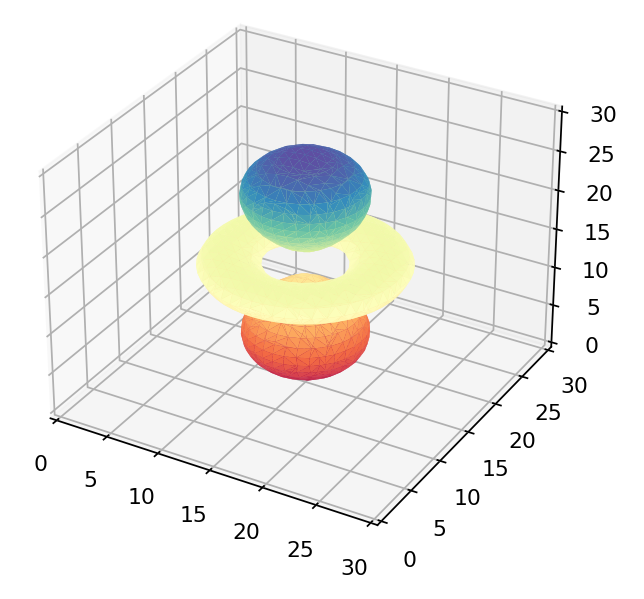 The |
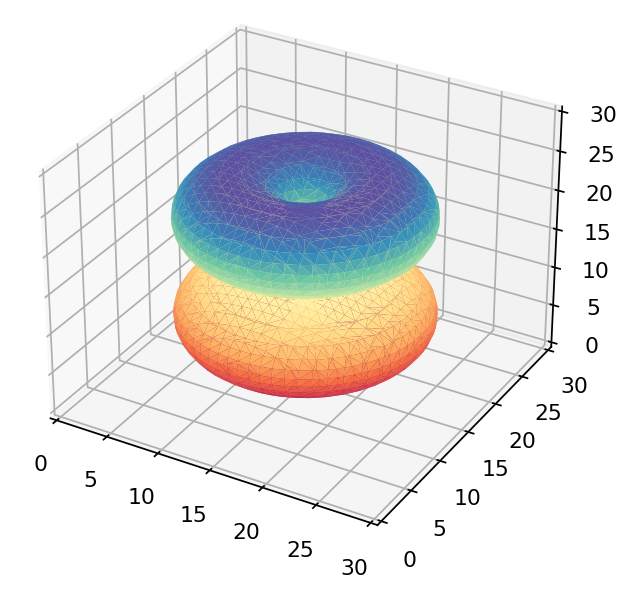 The |
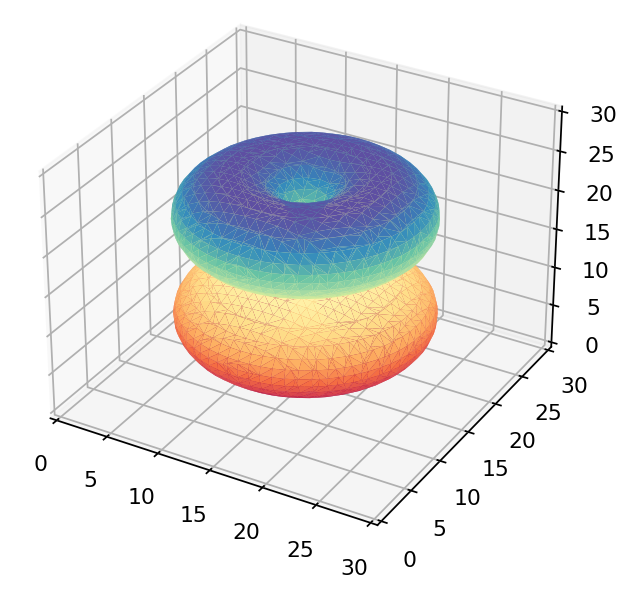 The |
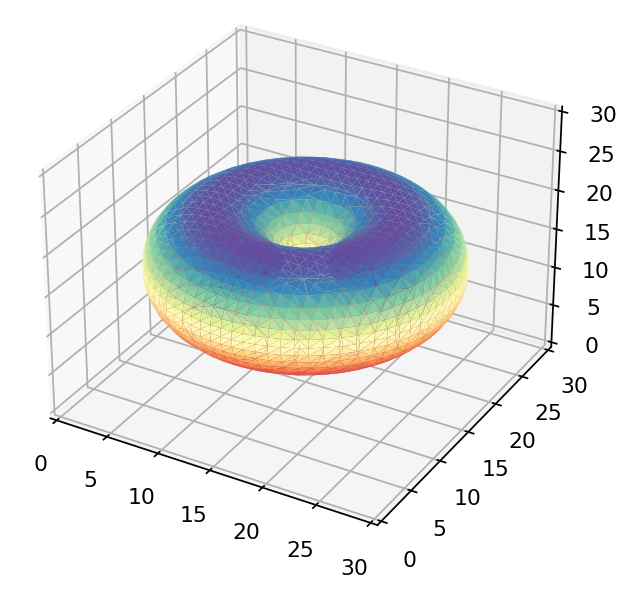 The |
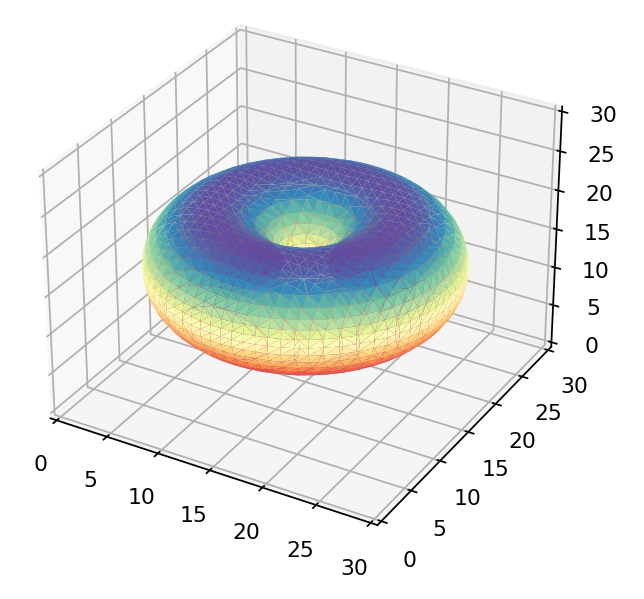 The |
Only the first of these looks like the 3d orbitals we see in chemistry textbooks as shown below! What’s going on?
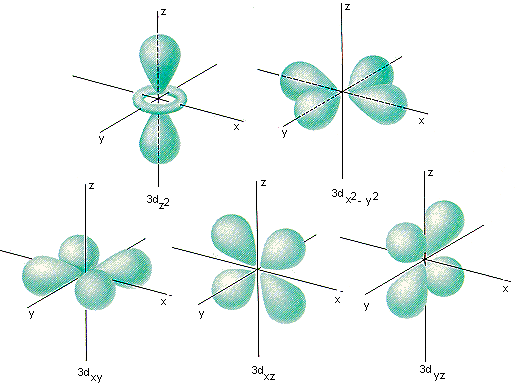
As it turns out while the is produced by
the
orbitals are produced by combinations of the other hydrogen 3d orbital solutions. What are these combinations? Well:
Now that we have the usual 3d orbital wavefunctions and can obtain the electron density at any arbitrary coordinate in space its time to start sampling some points!